Ανάλυση με την βοήθεια του στατιστικού προγράμματος R
Γιατί R; Το πρόγραμμα R δημιουργήθηκε το ως συνέχεια ενός εξαιρετικού στατιστικού προγράμματος του S-Plus. Θεωρείται, και όχι άδικα, ότι έχει σημαντικά δυσκολία χειρισμού των δεδομένων και εξαγωγής αποτελεσμάτων. Αυτή η δυσκολία όμως αποζημιώνεται από τα εξαιρετικής ποιότητας γραφικά αποτελέσματα τα οποία παραμετροποιούνται πλήρως και τις έτοιμες βιβλιοθήκες που καλύπτουν όλες τις μεθοδολογίες στατιστικής ανάλυσης. Θεωρείται ως από τα ποιο πολύτιμα εργαλεία των αναλυτών δεδομένων παγκόσμια, ενώ η προσπάθεια αυτή ενισχύεται και από τα πολλά forums ακαδημαϊκών και βιομηχανικών προγραμματιστών. Το πρόγραμμα μπορείτε να το κατεβάσετε από την ιστοσελίδα https://www.r-project.org/ και τις βιβλιοθήκες μπορείτε να τις κατεβάσετε μετά την εγκατάσταση του προγράμματος. Υπάρχουν πάρα πολλές ιστοσελίδες που μπορείτε να βρείτε έτοιμο κώδικα και οδηγίες για την χρήση σε όλες τις μεθόδους ανάλυσης ενώ για μια πρώτη προσέγγιση που καλύπτει σχεδόν όλες τι μοντέρνες μεθόδους ανάλυσης προτείνουμε το βιβλίο των Venables και Ripley «Modern Applied Statistics with S»
Στη συνέχεια ακολουθεί ένα δείγμα των δυνατοτήτων του R ενώ εάν θέλετε να κάνετε δοκιμές μπορείτε να κατεβάσετε τον κώδικα μετά από επικοινωνία.
Τα δεδομένα αφορούν τον ετήσιο αριθμό οδικών ατυχημάτων για την περίοδο 1991 εώς και 2015 και σύμφωνα με την ΕΛΣΤΑΤ
Ανάλυση χρονικών σειρών
Η ανάλυση χρονικών σειρών με την βοήθεια του R περιέχει ένα σημαντικό αριθμό έτοιμων βιβλιοθηκών που αυτοματοποιούν τις διαδικασίες και καλύπτουν όλη τη θεωρία.
Έλεγχος κανονικότητας
Στα επόμενα γραφήματα παρατηρούμε απόκλιση από την καμπύλη της κανονικότητα των δεδομένων
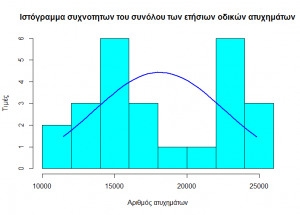
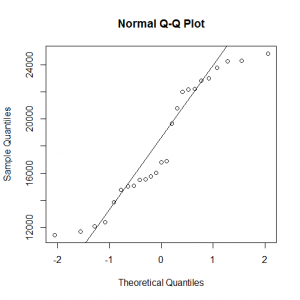
Ενώ το τεστ κανονικότητας των Kolmogorov – Smirnov μας ενημερώνει ότι τα δεδομένα ακολουθούν την κανονική κατανομή σε σ.σ. 1%
One-sample Kolmogorov-Smirnov test
data: tot
D = 0.16703, p-value = 0.4405
alternative hypothesis: two-sided
Η συμπεριφορά των οδικών ατυχημάτων δείχνει μια απότομη μείωση κατά την περίοδο 1998 έως και 2004. Η γενική τάση είναι πτωτική και χαρακτηρίζεται από κυκλική συμπεριφορά 10 ετίας 1991 – 2004 και 2005 – 2015.
Η συμπεριφορά αυτή γίνεται περισσότερο κατανοητή και με την βοήθεια του παρακάτω γραφήματος.
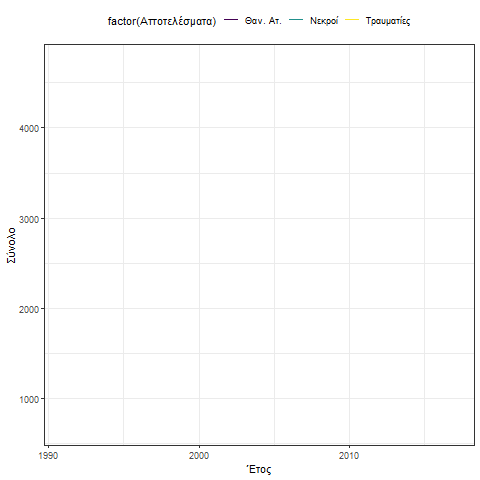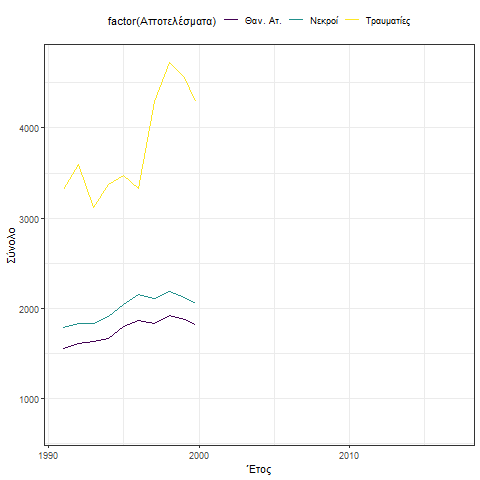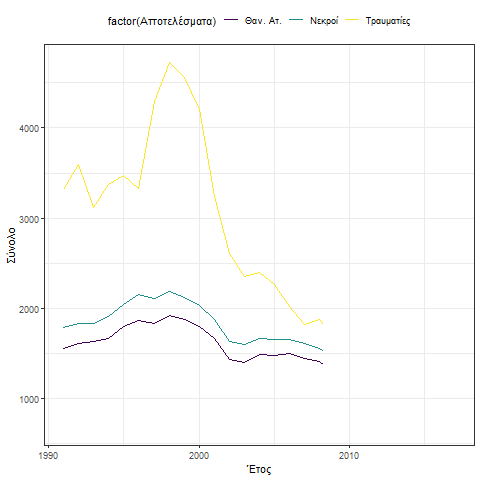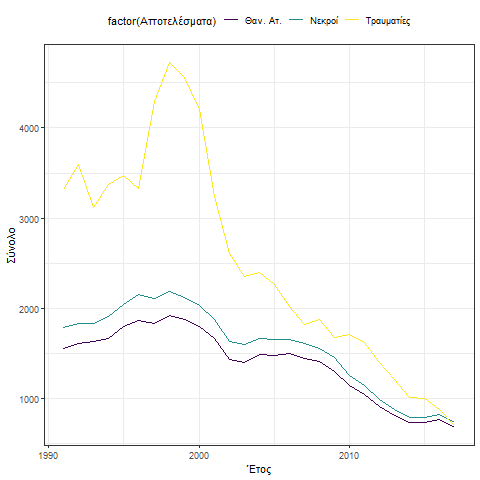
Η λείανση στης χρονικής σειράς, δηλαδή εύρεση των επιμέρους τάσεων που την επηρεάζουν δείχνει ότι μια σταθερή βραχυχρόνια τάση χωρίς επιμέρους διακυμάνσεις ή κυκλικές επαναλήψεις και την καθοδική γραμμική τάση μετά το 2015.
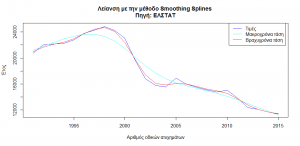
Μια συνήθης τεχνική για την μείωση της τάξης μεγέθους των τιμών της σειράς είναι η μετατροπή των τιμών με την βοήθεια του λογαριθμικού μετασχηματισμού. Λόγοι για αυτού του είδους τον μετασχηματισμό είναι η εξομάλυνση της συμπεριφοράς της χρονικής σειράς και η σύγκριση μεταξύ σειρών με διαφορετικές τιμές.
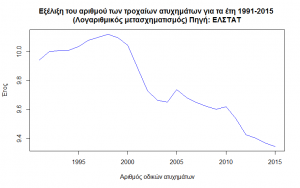
Η απαλοιφή της τάσης επιτυγχάνεται με τις πρώτες διαφορές δηλαδή την διαφορά της επόμενης μείον της προηγούμενης τιμής. Στο γράφημα των πρώτων διαφορών παρατηρούμε ότι η τάση έχει απαλειφθεί και ότι τα δεδομένα κινούνται γύρω από μια τιμή κοντά στο 0.
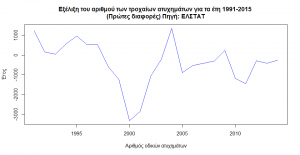
Η προηγούμενη προσέγγιση δεν έχει φέρει το επιθυμητό αποτέλεσμα της απαλοιφής της τάσης καθώς παρατηρείται και επιμέρους και συνολική τάση. Οι δεύτερες διαφορές δεν δείχνουν να έχουν και πάλι την αναμενόμενη εικόνα της σταθερής κίνησης των δεδομένων γύρω από μια τιμή.

Εύρεση σημείων απότομων αλλαγών της σειράς
Η εύρεση των σημείων στα οποία η χρονική σειρά έχει κάνει ένα επαρκή αριθμό αλλαγών στις τιμές της ώστε να δώσει σημάδι ότι αλλάζει η αθροιστική της τιμή παρουσιάζεται στο παρακάτω γράφημα από όπου βλέπουμε ότι το έτος κατά το οποίο η μεταβολή των δεδομένων αλλάζει συμπεριφορά είναι το 2012.
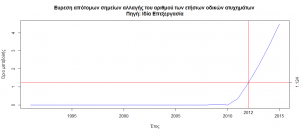
Το διάγραμμα των αυτοσυσχετίσεων ACF και μερικών αυτοσυσχετίσεων PACF δείχνει ότι ένα κατάλληλο μοντέλο για αυτή την χρονική σειρά είναι το ARIMA(0,1,1)

Τα διαγνωστικά αυτού του μοντέλου δείχνουν ότι
1.Τα υπόλοιπα ακολουθούν την κανονική κατανομή
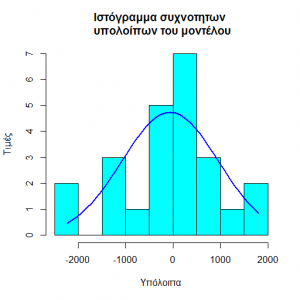
Το οποίο επιβεβαιώνεται και από το τεστ των Shapiro – Wilk
Shapiro-Wilk normality test
data: fit1$resid
W = 0.96244, p-value = 0.4893
2.Τα υπόλοιπα δεν σχηματίζουν μια αυτοπαλίνδρομη χρονική σειρά (ACF of Residuals) και σύμφωνα με το Ljung – Box – Pierce Statistic το μοντέλο κρίνεται επαρκές.
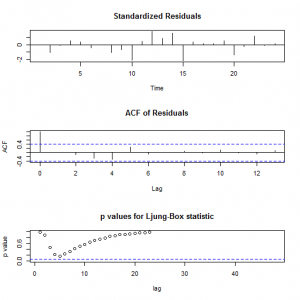
Ένα πιθανό υποψήφιο μοντέλο που θα μπορούσε να περιγράψει αυτή την χρονική περιγράφεται από την εξίσωση Ŷt = μ + Yt-1 – θ1et-1
και με την αντικατάσταση των αριθμητικών συντελεστών μετατρέπεται στο
Ŷt = -388.5 + Yt-1 +0.014et-1
Το μοντέλο παρουσιάζει σημαντικά μειονεκτήματα όπως η ισχυρή επιρροή της μέσης τιμής (σταθερά) η οποία αναγκάζει τον συντελεστή να πάρει θετική τιμή.
Συμπέρασμα
Το μοντέλο χρειάζεται επανεξέταση και πιθανή αφαίρεση του σταθερού όρου για ασφαλείς προβλέψεις.

